Tidy Tuesday: Women’s Football

statistics
tidy tuesday
sports
football
Authors

Kate Pyper

Brendan Clarke

Kennedy

Imran

Abram

Jon

Published

July 17, 2024

After a bit of a (in Jon’s view) dearth of interesting datasets within Tidy Tuesday, this week brought something worth looking at to the table: datasets on women’s football over the last few years, including changes in its popularity, as measured by attendance.

Kate led this session.

Setting up

Code 
library(tidyverse)
library(broom)

tuesdata <- tidytuesdayR::tt_load(2024, week = 29)

ewf_appearances <- tuesdata$ewf_appearances
ewf_matches <- tuesdata$ewf_matches
ewf_standings <- tuesdata$ewf_standings

Questions, questions…

Firstly, we decided to look at growth attendance over time:

Code 
ewf_matches %>% 
  group_by(season) %>% 
  summarise(attendance = median(attendance, na.rm = TRUE)) %>% 
  ggplot() +
  geom_col(aes(x = season, y = attendance)) +
  theme(axis.text.x = element_text(angle = 90))

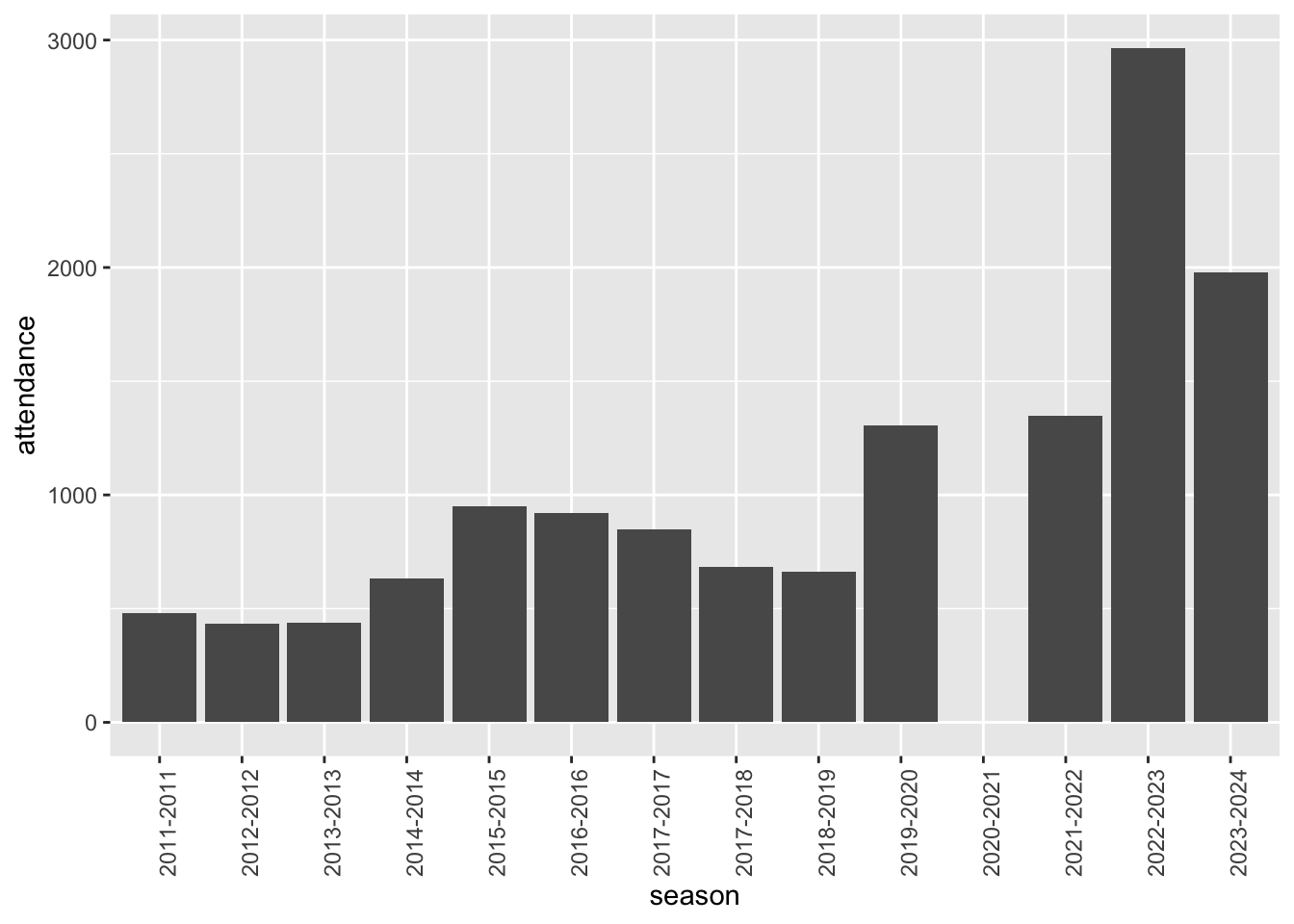
For some reason, there was no attendance in the 2020-2021 season. Definitely something unexpected that we should investigate further, as 2020 was a completely normal year in every way

What about trends in season, e.g. are the first matches more popular than the rest, much like the first episodes of TV series tend to be watched more than the rest of the series?

Code 
ewf_matches %>% 
  group_by(season) %>% 
  mutate(match_no = order(date)) %>% 
  ggplot(aes(x = match_no, y = attendance, colour = season, group = season)) +
  geom_point() +
  facet_wrap(~ tier, scales = "free") +
  scale_y_log10()

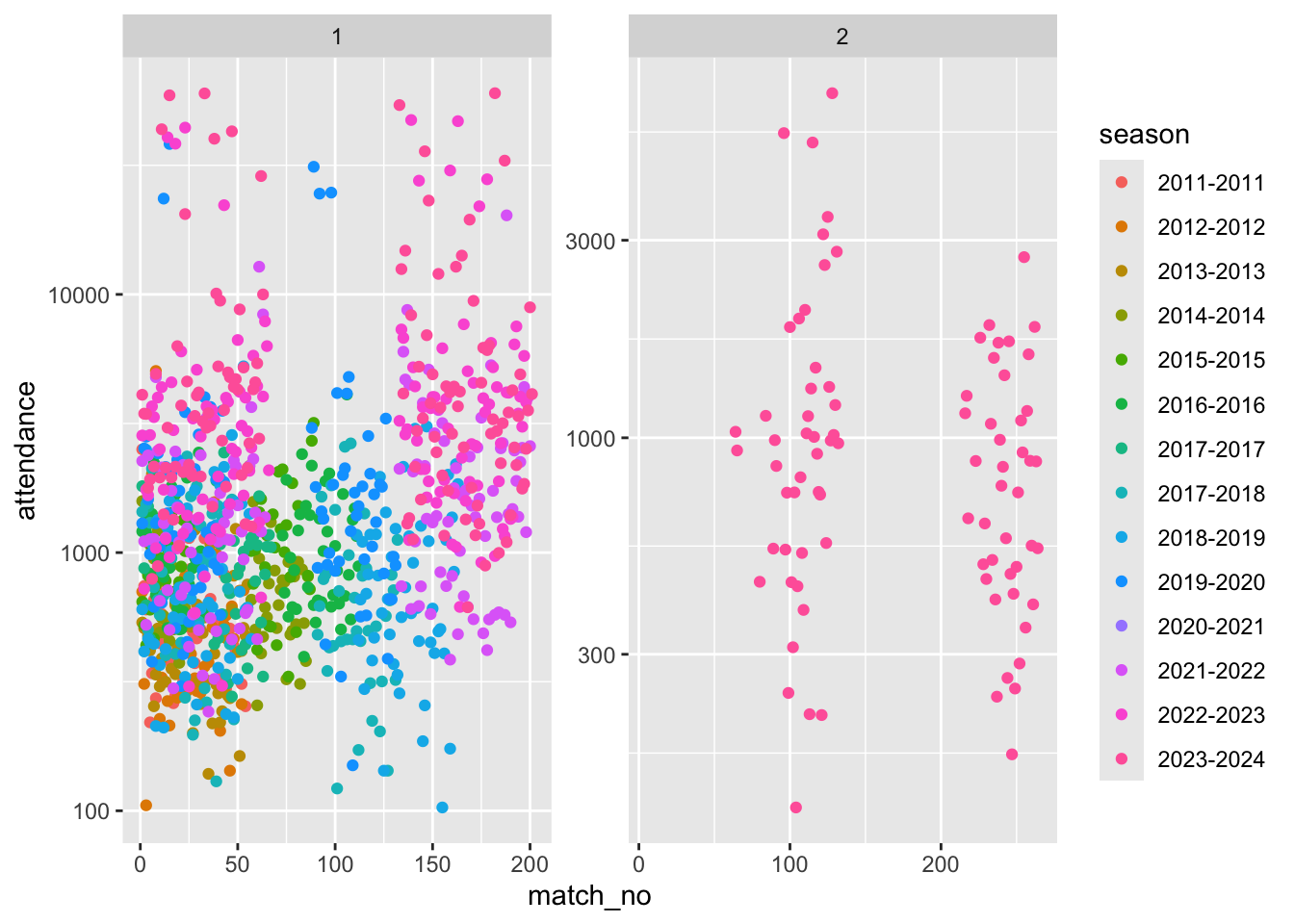
Note we used a log y scale as attendance seems to be very variable between matches. However we couldn’t see any obvious trend within season.

We also decided just to focus on tier 1

Code 
ewf_matches %>% 
  filter(tier == 1) %>% 
  group_by(season) %>% 
  mutate(match_no = order(date)) %>% 
  ggplot(aes(x = match_no, y = attendance, colour = season, group = season)) +
  geom_point() +
  scale_y_log10()

Modelling

We then decided to try to model factors that could predict (log) attendance. First a model predicting log-attendance on home team id, match number, and season, but without interaction terms. And then a model with interaction terms:

Code 
ewf_matches %>% 
  filter(tier == 1) %>% 
  group_by(season) %>% 
  mutate(match_no = order(date)) %>% 
  lm(log10(attendance) ~ home_team_id + match_no + season, data = .) ->
  mod1

ewf_matches %>% 
  filter(tier == 1) %>% 
  group_by(season) %>% 
  mutate(match_no = order(date)) %>% 
  lm(log10(attendance) ~ home_team_id + match_no + season + season*match_no, data = .) ->
  mod2

How to compare? Well, as mod1 can be considered as a restricted version of mod2 (the interaction term coefficents set to 0) we can use ANOVA to see if the additional complexity of the unrestricted model, mod2, is ‘worth it’:

Code 
anova(mod2)
Analysis of Variance Table

Response: log10(attendance)
                 Df Sum Sq Mean Sq F value    Pr(>F)    
home_team_id     17 63.340  3.7259 42.4441 < 2.2e-16 ***
match_no          1  4.241  4.2414 48.3166 6.604e-12 ***
season           12 56.470  4.7058 53.6073 < 2.2e-16 ***
match_no:season  12  1.508  0.1257  1.4314    0.1453    
Residuals       982 86.203  0.0878                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Code 
anova(mod1, mod2) # same as above but pulls out specific test that we are interested in
Analysis of Variance Table

Model 1: log10(attendance) ~ home_team_id + match_no + season
Model 2: log10(attendance) ~ home_team_id + match_no + season + season * 
    match_no
  Res.Df    RSS Df Sum of Sq      F Pr(>F)
1    994 87.711                           
2    982 86.203 12    1.5079 1.4314 0.1453

We concluded:

Interaction term not significant - proceed with mod1

Now to look at the coefficients on mod1:

Code 
summary(mod1)

Call:
lm(formula = log10(attendance) ~ home_team_id + match_no + season, 
    data = .)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.90496 -0.19277 -0.03661  0.14062  1.51043 

Coefficients:
                      Estimate Std. Error t value Pr(>|t|)    
(Intercept)          2.9890968  0.0541578  55.192  < 2e-16 ***
home_team_idT-002-T -0.2686225  0.0619191  -4.338 1.58e-05 ***
home_team_idT-003-T -0.3359697  0.0446896  -7.518 1.24e-13 ***
home_team_idT-005-T -0.2652441  0.0524152  -5.060 4.98e-07 ***
home_team_idT-006-T -0.2461753  0.0464112  -5.304 1.39e-07 ***
home_team_idT-008-T -0.0507938  0.0425091  -1.195 0.232413    
home_team_idT-011-T -0.4073355  0.0693986  -5.870 5.95e-09 ***
home_team_idT-013-T -0.5394900  0.0448460 -12.030  < 2e-16 ***
home_team_idT-014-T -0.2734024  0.0619209  -4.415 1.12e-05 ***
home_team_idT-016-T -0.2675245  0.0598158  -4.472 8.62e-06 ***
home_team_idT-017-T -0.3209426  0.0440625  -7.284 6.60e-13 ***
home_team_idT-020-T -0.0394211  0.0447805  -0.880 0.378900    
home_team_idT-021-T  0.0452529  0.0575592   0.786 0.431939    
home_team_idT-023-T -0.4128162  0.0497442  -8.299 3.40e-16 ***
home_team_idT-027-T -0.4112510  0.0693942  -5.926 4.27e-09 ***
home_team_idT-028-T -0.3241747  0.0575895  -5.629 2.36e-08 ***
home_team_idT-030-T -0.3459956  0.0530576  -6.521 1.11e-10 ***
home_team_idT-031-T -0.3978321  0.0708242  -5.617 2.52e-08 ***
match_no            -0.0002474  0.0003161  -0.783 0.434030    
season2012-2012     -0.0706150  0.0641552  -1.101 0.271298    
season2013-2013     -0.0381315  0.0604345  -0.631 0.528215    
season2014-2014      0.0752879  0.0611843   1.231 0.218797    
season2015-2015      0.2112739  0.0626453   3.373 0.000774 ***
season2016-2016      0.2591016  0.0582373   4.449 9.60e-06 ***
season2017-2017      0.1782820  0.0691801   2.577 0.010107 *  
season2017-2018      0.1231090  0.0579269   2.125 0.033812 *  
season2018-2019      0.1606422  0.0562308   2.857 0.004368 ** 
season2019-2020      0.4160694  0.0578761   7.189 1.28e-12 ***
season2021-2022      0.3912164  0.0568712   6.879 1.06e-11 ***
season2022-2023      0.7350856  0.0570183  12.892  < 2e-16 ***
season2023-2024      0.8347182  0.0565907  14.750  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.2971 on 994 degrees of freedom
  (178 observations deleted due to missingness)
Multiple R-squared:  0.5858,    Adjusted R-squared:  0.5733 
F-statistic: 46.86 on 30 and 994 DF,  p-value: < 2.2e-16

We had some fun trying to find the most and least popular teams. The reference team, team 1, happens to be about the most popular team.

Code 
ewf_appearances %>% 
  filter(season == "2023-2024") %>% 
  select(team_id, team_name) %>% 
  distinct() %>%
  arrange(team_id) |>
  view()

We thought we could do more to visualise the difference in apparent popularity between teams, producing some ‘tie fighter’ graphs (also known as blobograms, apparently)

Code 
tidy(mod1) %>% 
  filter(str_detect(term, "home_team")) %>% 
  mutate(term = str_remove(term, "home_team_id")) %>% 
  ggplot() +
  geom_point(aes(x = estimate, y = term)) +
  geom_errorbarh(aes(xmin = estimate - 2*std.error, xmax = estimate + 2*std.error, y = term)) +
  geom_vline(aes(xintercept = 0), linetype = "dashed")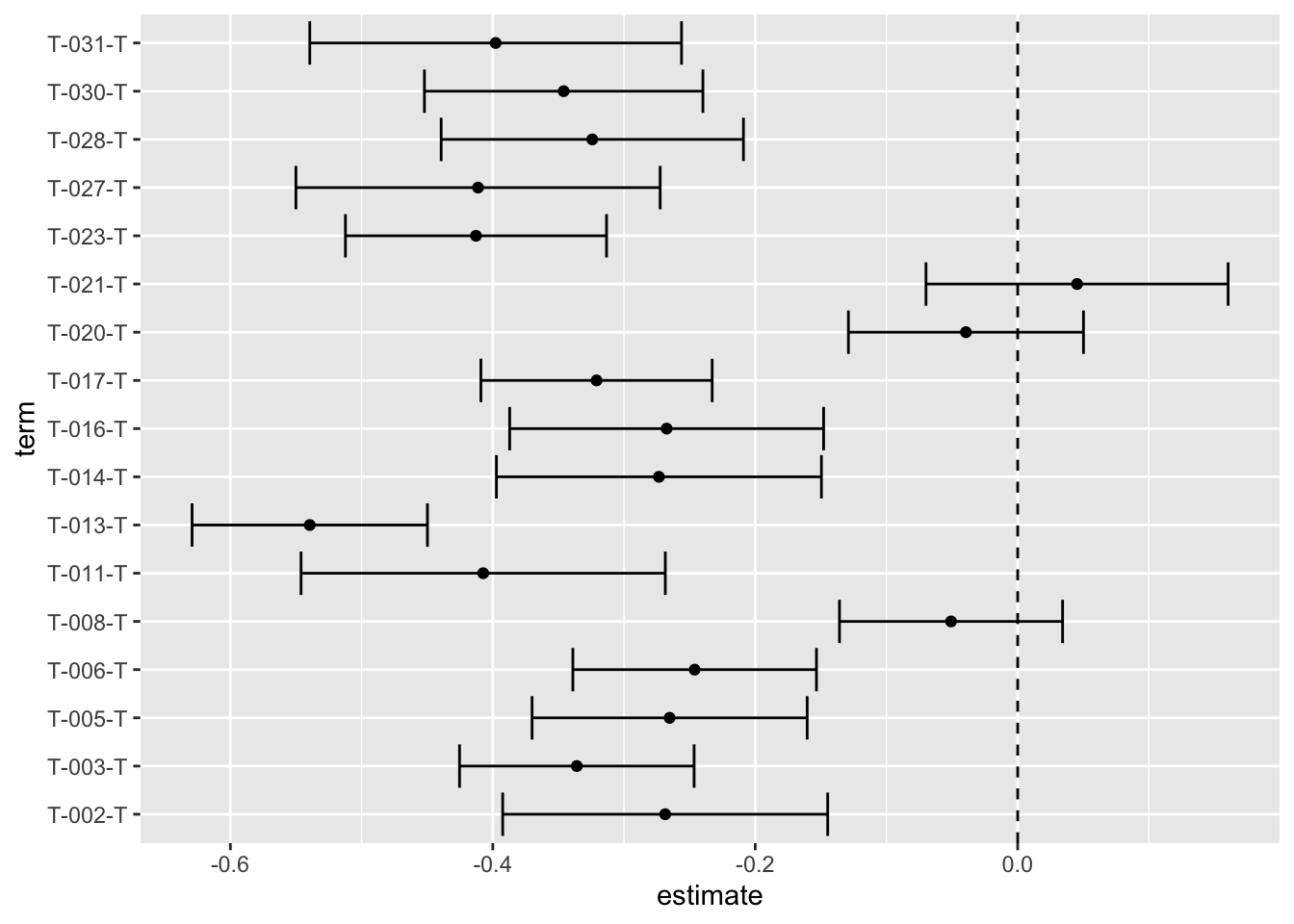

Poor old team 13! (Everton Women)

Compared with the reference team (Arsenal Women) only 3 teams looked similarly popular: team 8 (Chelsea Women), team 20 (Manchester City), and team 21 (Manchester United).

Then we decided to do the same kind of thing for season, which should showing growing popularity over time:

Code 
tidy(mod1) %>% 
  filter(str_detect(term, "season")) %>% 
  mutate(term = str_remove(term, "season")) %>% 
  ggplot() +
  geom_point(aes(x = estimate, y = term)) +
  geom_errorbarh(aes(xmin = estimate - 2*std.error, xmax = estimate + 2*std.error, y = term)) +
  geom_vline(aes(xintercept = 0), linetype = "dashed")

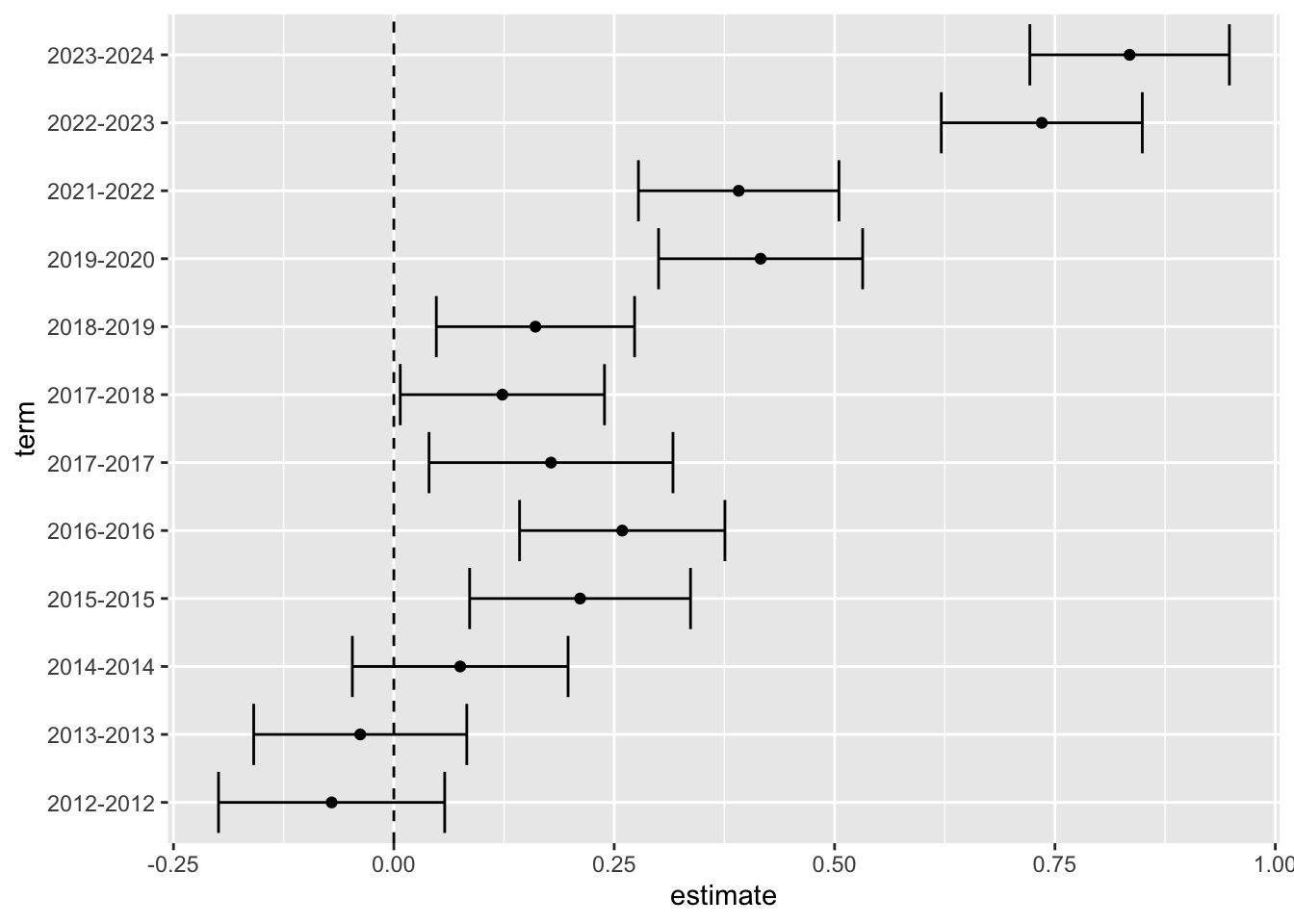
Up, up and away! (mostly…)

Conclusion

Some places to go:

  • Why the decline in 2016, 2017, 2018?
  • What caused the jumps in 2015, 2019, 2022?